
Grades K-2, 3-5

Don't have an account yet? Sign up for free
Don't have an account yet? Sign up for free
Nearpod version available
Students will be able to:

In this personal finance lesson, students will learn how productivity and government policy influences the distribution of income.
The personal distribution of income is the way analysts organize income by categories such as households, families, or even individuals. The level of income usually depends on the productivity of workers and other factors that affect the structure of the economy, such as government policies, technology, or discrimination. Differences in productivity across individuals can contribute to income inequality.
Mathematics and statistics provide tools to analyze the distribution of income and income inequality. The mean and median provide measures of central tendency for the distribution of income. The Lorenz curve graphically represents the distribution of income across a population. While the mean and median condense information about the income distribution to single summary statistics, the Lorenz curve provides more perspective about the distribution of income. Comparisons between different income distributions can be made by analyzing differences in statistics, such as the mean and median, and the Lorenz curve. For example, comparing the mean and median income of people in an economy is common. Using median income can avoid some of the pitfalls of averages.
Changes in productivity and structural factors like government policies can alter the distribution of income. Government often uses policies to redistribute income to reduce income inequality. Government taxation is one means of redistributing income. Progressive income taxes, for example, redistribute income in favor of lower income households. Redistribution of income can also occur through a transfer of income, spending and assistance programs, and programs designed to provide training to workers. A goal of reducing income inequality might involve transferring money from higher-income groups to lower-income groups. While some redistribution policies may increase income for some groups, some of these policies, at the same time, may distort economic incentives by weakening the relationship between productivity and income. Other policies could have different effects.
Mathematics and statistics also provide ways to effectively analyze the level of income equality and changes in the distribution of income. Changes in the distribution of income can be reflected in changes in measures of central tendency, such as the mean and median, as well as changes in a Lorenz curve. Income inequality can be measured by comparing measures of central tendency and by calculating a Gini coefficient based on a Lorenz curve. The degree of income inequality is quantified by a Gini coefficient, and changes in the value of the Gini coefficient indicate changes in income inequality.
|
Sharon |
Michael |
Jordan |
Allison |
|
$20,000 |
$35,000 |
$60,000 |
$85,000 |
Short Answer:
The Lorenz curves for two different income distributions are shown in the following graphs:
Graph 1
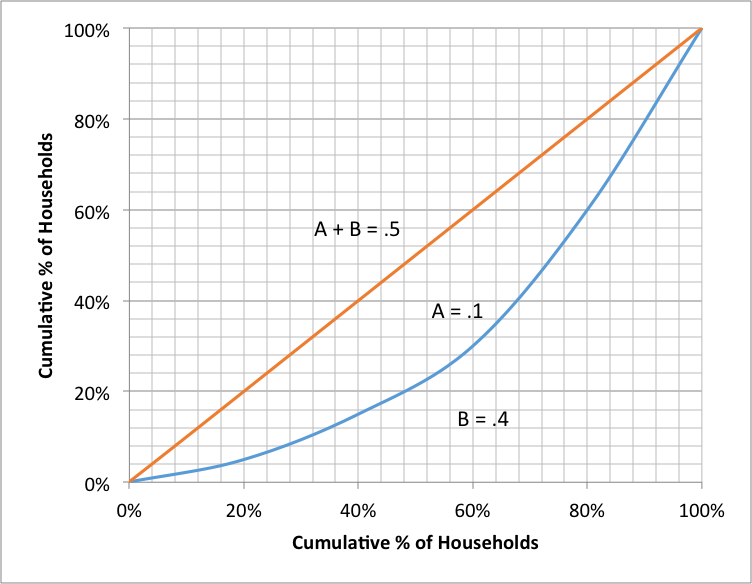
Graph 2
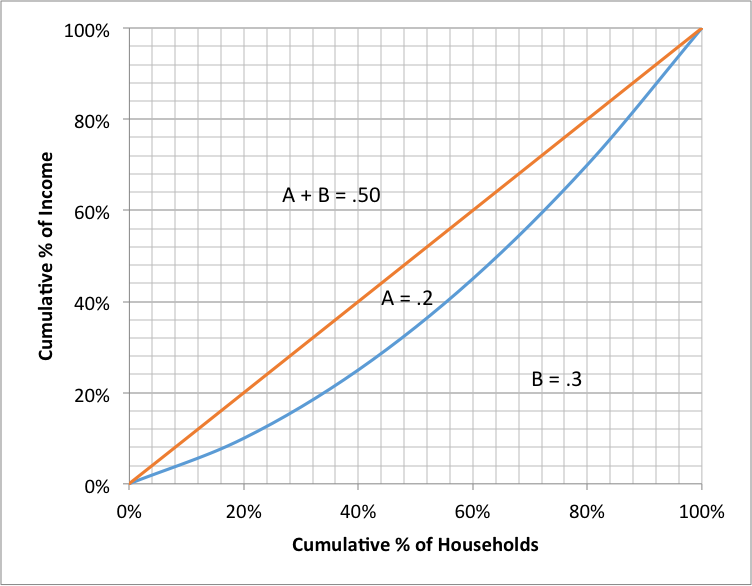

Grades K-2, 3-5

Content Partner
Grades Higher Education, 9-12

Grades 9-12

Grades 9-12
