
Grades 9-12

Don't have an account yet? Sign up for free
Don't have an account yet? Sign up for free
Nearpod version available
Students will be able to:

In this personal finance lesson, students explore budget constraints by solving a contextual problem.
Budgets are an important part of personal finance and meeting financial goals. While a budget is a spending and saving plan, based on estimated income and expenses for an individual or an organization over a specific time period, budget constraints are limits. Goods are tangible objects and services are activities that people perform for us. Both satisfy economic wants. The prices of goods and services and the amount of personal income-(i.e., payments earned by households for selling or renting their productive resources which may include salaries, wages, interest and dividends)-limit spending and serve as constraints to budgets. This lesson considers a problem situation in which only two goods can be purchased with a given income. This simplified approach should enable students to extend the decision-making process to more complex (e.g., real-world) challenges virtually everyone faces. The budget line is represented using tables, graphs, and linear functions. Equations use constants and variables to represent relationships between quantities. Variables are symbols used to represent numbers. The impact of shifts in income and prices of goods can be analyzed by exploring transformations of the budget line that represent relationships between these quantities.
Review the key points of the lesson using the following questions:
a. 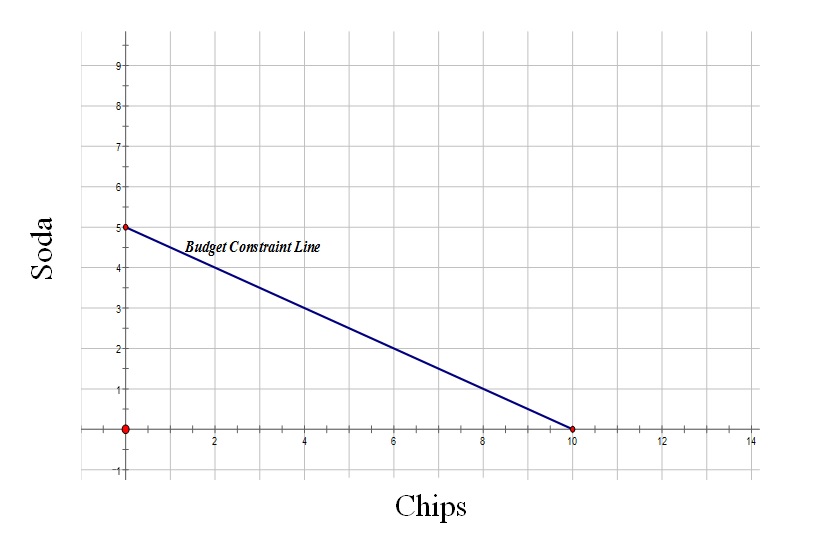
b. 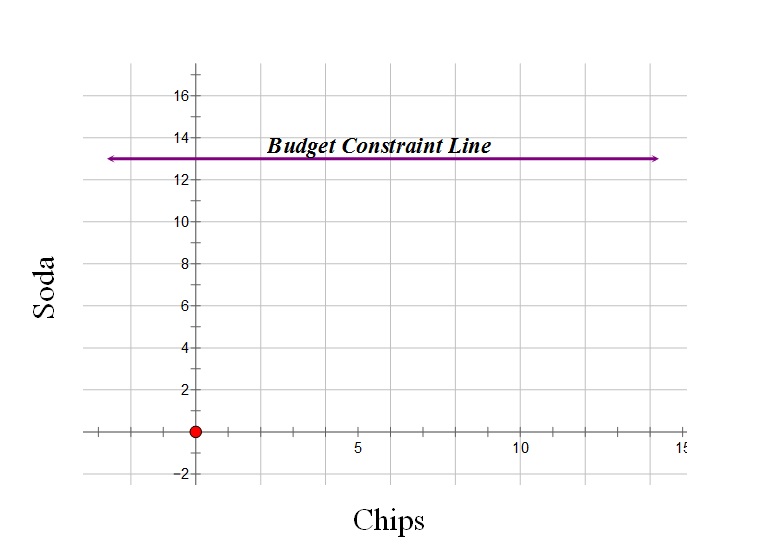
c. 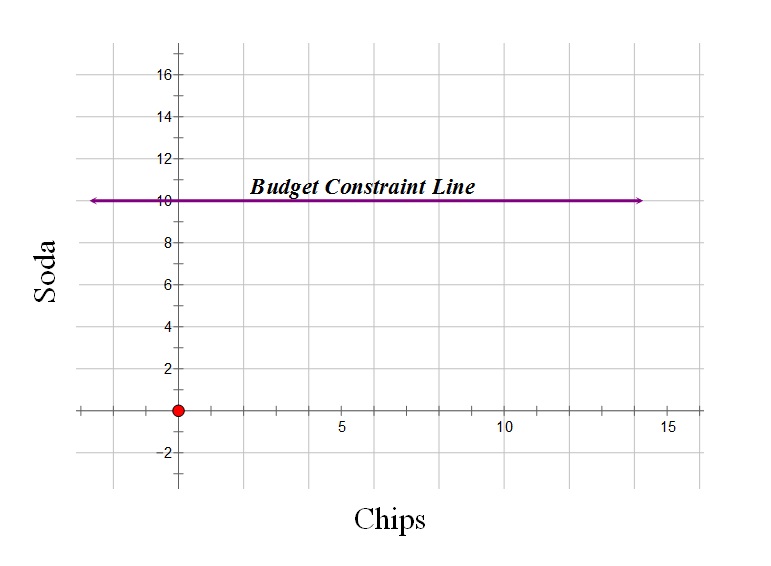
d. 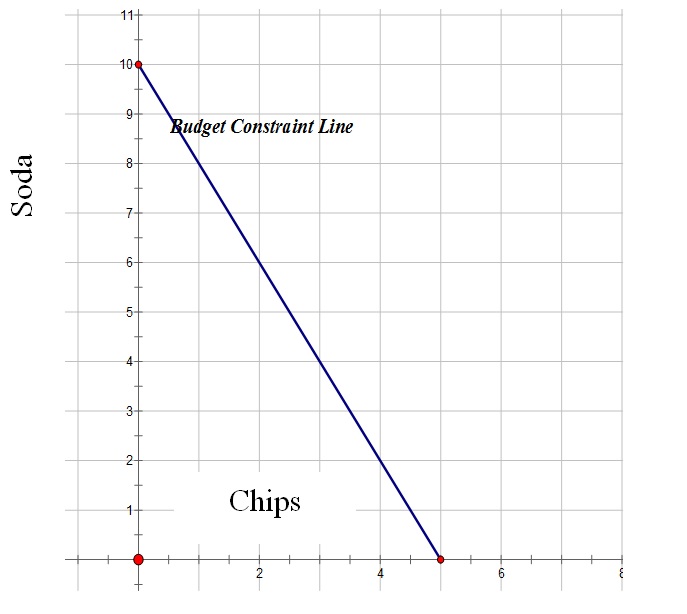
[Answer: a.]
Answer:
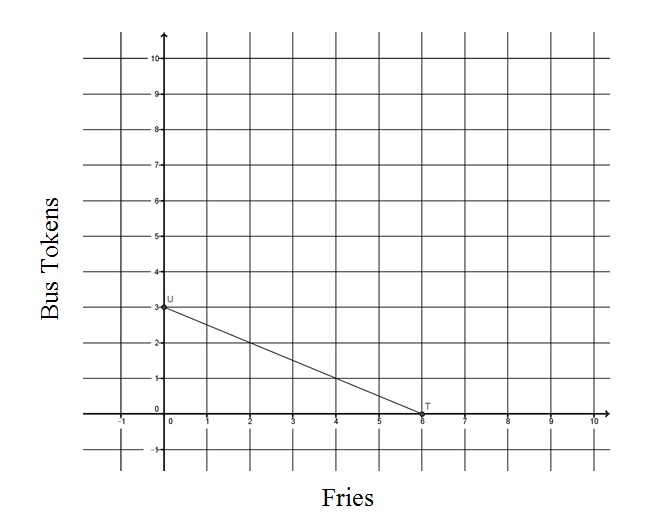

Grades 9-12

Grades 9-12

Grades 9-12

Content Partner
Grades 6-8, 9-12
