
Grades 9-12

Don't have an account yet? Sign up for free
Don't have an account yet? Sign up for free
Nearpod version available
Students will be able to:

In this personal finance lesson, students will make a connection between derivatives and marginalism.
Profit maximizing firms use marginal analysis to determine whether to produce an additional unit of output or to employ an extra resource. In its most basic sense marginal cost is simply a measure of the rate of change between the total costs and the quantity of output (or in another context the amount of a variable input). Using the metric of cost this lesson explores the concept of slope from an economic point of view.
The lesson uses Marginal Costs and Marginal Revenue as context for the underlying meaning of the derivative function. Students make the connection between the difference quotient and marginalism leading to the application of derivatives to find marginal functions. Students also apply their findings to a firm’s marginal functions to decide how much the firm should produce to maximize profit.
Ex. 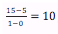 for production of 1st item.
for production of 1st item.
Ex. 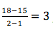 for production of 2nd item.
for production of 2nd item.

Grades 9-12

Grades 9-12

Grades 9-12

Grades 9-12
